COVID-19, le « bon sens » et le théorème de Bayes…
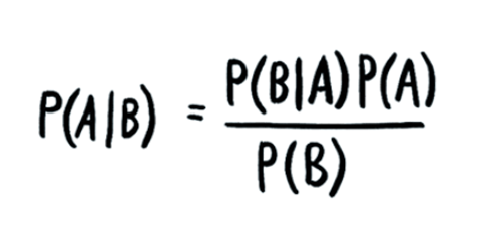
Quelquefois, avec ce que nous appelons le "bons sens" on se fourvoie totalement. Les croyances issues de ce "bon sens" n'ont alors rien à voir avec la réalité. En voici la preuve avec l'exemple des tests COVID-19.
Ce que vous allez lire n'est pas une opinion sur les tests, mais l'application d'une simple formule mathématique démontrée par Thomas Bayes autour de 1760. Elle sert comme fondement pour toutes les "inférences bayésiennes" liées aux prises de décision lorsqu'on dispose uniquement d’éléments incertains (sous forme de % de probabilité). Elle est également la base des traitements des intelligences artificielles.
Supposons que l'on teste 10000 personnes, dont, supposons que 1% seulement soit vraiment malade. Supposons que le test soit fiable à 95% (ce chiffre moyen provient du site de la Haute Autorité de Santé: la HAS retient par exemple : la présence d’un marquage CE, la valeur seuil minimale de la sensibilité clinique (probabilité d’avoir un test positif si le sujet est malade, c’est-à-dire vérifier que le test détecte bien la présence des anticorps anti-SARS-CoV-2 dans le sang de patient COVID-19) estimée à 90% ou 95% en fonction de l’usage du test, ou encore la valeur seuil minimale de spécificité clinique (probabilité d’avoir un test négatif chez les non-malades, c’est-à-dire vérifier si le test est bien négatif en l’absence d’anticorps anti-SARS-CoV-2 dans le sang de donneurs non infectés) estimée à 98 %. )
Sur 10000 personnes, disons que 100 personnes (1%) sont vraiment malades et 9900 personnes sont saines. Appliquons le test avec son taux très bon de réussite de 95%:
Sur les 9900 (99%) personnes saines : 9900 x 95% vont être testées saines soit 9405 et 495 (5%) testées positives (malades). Et sur les 100 personnes malades: 95 vont être testées malades et 5 saines.
Au total, d’après le test fiable à 95% il y aurait 495+95=590 personnes testées positives (malades).
95 personnes malades sur 590 issues des tests cela donne environ 16% d’avoir contracté effectivement la maladie parmi les personnes testées positives ! La réponse de "bon sens populaire" aurait été "j'ai 95% de chances d'avoir contracté la maladie". En fait "être positif" est faux dans 84% des cas ! Et ceci avec un test fiable à 95%.
C'est ce que nous dit le théorème de Bayes: Lorsque un phénomène est marginal (quelques%) par rapport à la grande majorité des cas, plus on teste la population, plus on obtiendra de faux cas positifs !
La deuxième chose que nous dit le théorème de Bayes est que seul l'environnement précis, les méta-données qui décrivent la "fiabilité" d'un pourcentage, d'une probabilité (en l’occurrence la fiabilité des tests), permet de se faire une idée d'un phénomène statistique et de prendre des décisions adaptées.